Revisiting the laminar plume

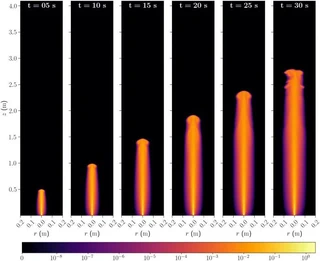
We revisit the classical problem of a laminar plume arising from a point source of heat on a horizontal boundary of infinite extent in an otherwise motionless neutrally stratified environment. The Boussinesq equations of motion and thermal energy for a steady axisymmetric plume are approximated separately for the plume interior and exterior, with the two regions connected via pressure continuity and use of the transverse (radial) equation of motion, an equation that has not been used in previous theoretical analyses of laminar plumes. An analysis of the governing equations yields a simple relation between the azimuthal vorticity and buoyancy, two variables of prime interest in studies of axisymmetric thermals, plumes, and jets. The relation states that when the Prandtl number is 1, the vorticity is equal to the buoyancy times radius divided by twice the kinematic viscosity. A more complex vorticity–buoyancy relation is obtained for arbitrary Prandtl numbers. The same vorticity–buoyancy relations are predicted for the plume interior and exterior. The relation for a Prandtl number of 1 is validated using output from a direct numerical simulation of a laminar plume induced by a small heat source on the lower boundary. The steady—state vorticity–buoyancy relation is confirmed in regions that have attained a steady state and also, remarkably, at earlier times, where the plume cap has passed, but the flow is still evolving.

Journal article

Physics of Fluids, 37(4), 1–13